\n"); $doctype = "XHTML5"; } else { header("Content-type: text/html; charset=utf-8"); $doctype = "HTML5"; } ?> CS-343 Assignment 4 Solutions

CS-343 Assignment 4
Solutions

Solutions

  1. Write the complete equation for c2 using carry-lookahead logic. That is, the only variables you can use are c0, g0, p0, g1, and p1. (The answer is in the textbook.)
    c2 = g1 + p1g0 + p1p0c0
  2. Rewrite the equation for c2 using only the only variables: a0, b0, c0, a1, b1. Note that you may not use c1 in the expression.
    c2 = a1b1 + a1a0b0 + b1a0b0 + a1b0c0 + a0b1c0
  3. Why must you not use c1 in the previous equation?
    It would introduce an additional level of propagation delays, defeating the purpose of carry-lookahead logic.
  4. Give the sum of products value for segment 1 of a seven segment display using sigma notation. For example: segment 0 is on for the digits 0, 2, 3, 5, 6, 7, 8, 9, A, C, E, and F, so the sum of products value for segment 0 using sigma notation would be Σ(0, 2, 3, 5, 6, 7, 8, 9, 10, 12, 14, 15).
    segment1 = Σ(0, 1, 2, 3, 4, 7, 8, 9, 10, 13)
  5. Use a Karnaugh Map to minimize the answer to the previous question.
    Assume the inputs, from left to right, are a, b, c, and d. There is more than one solution. Here is the Karnaugh Map before drawing in the circles. The rows are for a and b; the columns are for c and d.
    00011110
    001111
    011010
    110100
    101101
    One solution is: segment1 = a'b' + b'd' + a'c'd' + a'cd + ac'd Since I can’t easily draw the circles around the terms, here is a description of where each one goes and how it relates to the map: a'b' is the four cells in the top row b'd' is the four corner cells (you can do this: a student asked about it in class) a'c'd' is the two cells at in the left column of the first two rows a'cd is the two cells in the top two rows of the third column a'c'd is the two cells in the second column, bottom two rows
  6. Define arithmetic overflow for two’s complement numbers.
    Overflow is when the numerically correct result is not within the range of values that can be represented using the number n of bits available. That is, when the value of the result is outside the range: -2n-1 to +2n-1 - 1
  7. When is the Z condition code bit true?
    When the result is all zeros.
  8. When is the N condition code bit true?
    When the result is negative. That is, when the leftmost bit of the result (the sign bit) is 1.
  9. What is the bit-wise AND of 0xFFFF and 0x1234?
    0x1234
  10. What is the bit-wise OR of 0x1234 and 0x7DCB?
    0xFFFF
  11. What is the decimal value of the 16-bit two’s complement number 0xFFFC?
    -4
  12. What is the decimal value of the 16-bit two’s complement number 0x0064?
    +100
  13. Convert the 16-bit two’s complement number 0x89AB to the equivalent 32-bit number. Answer in hexadecimal.
    0xFFFF89AB
  14. Convert the 16-bit two’s complement number 0x789A to the equivalent 32-bit number. Answer in hexadecimal.
    0x0000789A
  15. What is the two’s complement of 0x1234? Answer in hexadecimal.
    0xEDCC
  16. What is the two’s complment of 0xFFFF? Answer in hexadecimal.
    0x0001
  17. What is the decimal value of the 16-bit two’s complement number, 0xFF85?
    -123
  18. What is the decimal value of the 16-bit two’s complement number, 0x0123?
    256 + 32 + 3 = 291
  19. Assume the slide switches are set to 011 101 1100 for Assignment 3.
    1. What is the binary value of A?
      011
    2. What is the binary value of B?
      101
    3. What is the binary value of A'?
      100
    4. What is the binary value of B'?
      010
    5. What is the binary result of ANDing A' and B'?
      000
    6. What is the binary result of ORing A' and B'?
      110
    7. What is the binary result of Adding A' + B' + C0
      111 (C0 is Bneg, which is 1.)
    8. What is the binary value of the SLTin inputs to the slices?
      001 (The leftmost bit of the previous answer is the rightmost bit of this one.)
    9. What are C2 and C3?
      0 and 0
    10. What are the names and values of the four condition code bits?
      C is 0 ( C3 ) V is 0 ( C3 ⊕ C2 ) N is 0 (This is based on the result, not on the sum) Z is 1 (See next answer)
    11. What is the result output of the ALU, in binary?
      000 (The AND result)
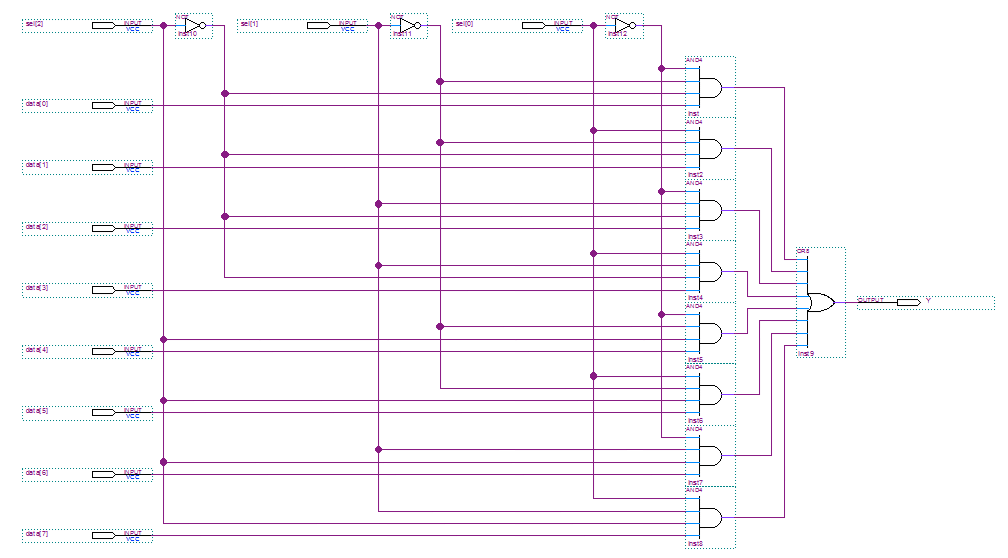
  20. Draw all the gates to implement an 8×1 multiplexer. If you submit the assignment on paper, you may draw the gates as a Quartus block diagram file and print the diagram. If you submit the assignment by email, you may submit the block diagram file itself. Be sure to include the input and output pins and to name them meaningfully. 8x1 Multiplexer Block Diagram