Exercise A-29

The Problem

Design a circuit that produces a 1 at the Z output when the input X changes from 0 to 1 or from 1 to 0, and that produces a zero at all other times. ... Show the state transition diagram, the state table, state assignment, and the final circuit using MUXes.

Analysis

We will use two state flip-flops, S₁ and S₀. S_0> will represent the most recently received value of X, and S₁ will represent the previous value. The state table looks like this:

Note that I have adopted the non-standard convention of labeling the arcs "X/Z", where Z is the output value in the state the arc comes from rather than the state the arc goes to. This convention makes it easier to design the circuit as a Moore Machine, in which the output value depends only on the current state.

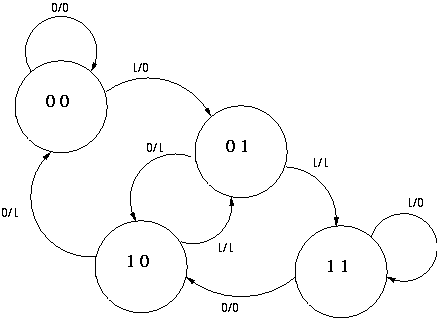
Using this convention, we can construct a state table looks like the following:

        Present External |  Next    External
         State   Inputs  |  State   Outputs
        ------------------------------------
         S₁  S₀    X      |  D₁ D₀      Y
        ------------------------------------
         0   0     0     |  0   0      0
         0   0     1     |  0   1      0
         0   1     0     |  1   0      1
         0   1     1     |  1   1      1
         1   0     0     |  0   0      1
         1   0     1     |  0   1      1
         1   1     0     |  1   0      0
         1   1     1     |  1   1      0

The first two rows of this table would be interpreted as follows: "If the present state is 00, the output is zero. If the external input during state 00 is 0, the next state will be 00 again, but if the external input is 1, the next state will be 01." The next two rows would be interpeted to say, "If the present state is 01, the external output is 1. If the external input is 0, the next state will be 10, but if it is 1, the next state will be 11.

We could minimize the three functions on the right side of the state table using Karnaugh Maps, but D₁ can be seen to be equal to S₀ by inspection, saving a bit of work. Likewise, D₀ can be seen by inspection to be the same as X. Finally, we can also see by inspection that Z is true if and only if S₁ is different from S₀, that is Z = S₁ xor S₀. Thus, the following circuit implements the entire state machine: